Introduction
In social research, statistical measures are essential for analyzing and interpreting data related to human behavior, social structures, and economic conditions. While the arithmetic mean is widely used, the geometric mean offers unique advantages in certain sociological contexts, particularly when dealing with skewed distributions, multiplicative relationships, and normalized growth rates.
This article explores the concept of geometric mean, its relevance in sociological research, and its applications in areas such as income inequality, population studies, and social indices. By understanding its utility, sociologists can make more accurate inferences about social phenomena.

What is Geometric Mean?
The geometric mean is a measure of central tendency that is particularly useful for datasets that are positively skewed or involve multiplicative processes. Unlike the arithmetic mean, which sums values and divides by the count, the geometric mean calculates the n-th root of the product of n values. Mathematically, for a dataset with *n* values (x₁, x₂, …, xₙ), the geometric mean (GM) is
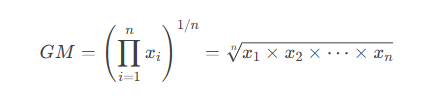
For logarithmic transformation (which linearizes multiplicative relationships), the formula can also be expressed as:
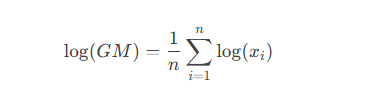
This property makes the geometric mean robust against extreme values, making it ideal for certain sociological measurements.
Why Use Geometric Mean in Social Research?
1. Handling Skewed Distributions
Many social datasets, such as income, wealth, and city sizes, follow a log-normal distribution rather than a normal distribution. In such cases, the arithmetic mean can be disproportionately influenced by extreme values (e.g., billionaires in income data), leading to misleading interpretations. The geometric mean provides a more balanced central tendency measure.
Example:
If five individuals have incomes of $10, $20, $30, $50, and $200, the arithmetic mean is $62, which overestimates the typical income due to the $200 outlier. The geometric mean, however, is approximately $34.8, offering a more realistic central value.
2. Multiplicative Growth Rates
Social phenomena such as population growth, economic development, and disease spread often follow exponential or multiplicative trends. The geometric mean is better suited for calculating average growth rates over time.
Example:
If a population grows by 10%, 20%, and 5% over three years, the arithmetic mean growth rate (11.67%) is incorrect for compounding effects. The geometric mean correctly gives the average growth rate as:
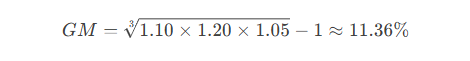
3. Normalization in Social Indices
Composite indices like the Human Development Index (HDI) and Gini coefficient often use geometric means to balance different scales (e.g., income, education, life expectancy). This prevents any single indicator from dominating the index.
Applications in Sociological Research
1. Income Inequality and Wealth Distribution
Income and wealth distributions are typically right-skewed, with a small percentage holding a large share of resources. The geometric mean helps in:
- Calculating median-equivalent averages that better reflect the majority’s economic condition.
- Comparing income disparities across groups without distortion from extreme outliers.
- Analyzing Pareto distributions (power-law distributions common in wealth studies).
Example:
The Gini coefficient, a measure of inequality, can be supplemented with geometric mean analysis to assess how income growth impacts different quintiles.
2. Health and Demographic Studies
In health research, variables like disease rates, hospital stays, and vaccination coverage often follow exponential patterns. The geometric mean helps in:
- Estimating average infection rates in epidemiology.
- Analyzing life expectancy trends where improvements are multiplicative.
3. Education and Test Scores
Standardized test scores sometimes exhibit log-normal distributions, especially in highly stratified education systems. Using the geometric mean can provide a fairer comparison of student performance across different socioeconomic backgrounds.
4. Urban Sociology and Population Density
City sizes and population densities often follow Zipf’s Law, where a few cities are disproportionately large. The geometric mean helps urban sociologists analyze typical city sizes without bias from megacities.
Limitations of Geometric Mean in Social Research
While the geometric mean is powerful, it has limitations:
- Not suitable for negative or zero values (since the product becomes zero or undefined).
- Less intuitive than the arithmetic mean for general audiences.
- Requires log transformation, which may complicate interpretation in some studies.
Geometric Mean vs. Other Measures
| Measure | Best Used When | Example in Sociology |
|---|---|---|
| Arithmetic Mean | Data is normally distributed | Average household size |
| Geometric Mean | Multiplicative growth, skewed data | Income distribution, population growth |
| Median | Extreme outliers present | Wealth inequality studies |
| Harmonic Mean | Rates and ratios | Average speed in migration studies |
Conclusion
The geometric-mean is a valuable yet underutilized tool in sociological research. Its ability to handle skewed distributions, multiplicative processes, and normalized indices makes it indispensable for analyzing income inequality, demographic trends, and social development metrics. While it is not a one-size-fits-all solution, its appropriate application can lead to more accurate and meaningful sociological insights.

As social scientists continue to grapple with complex, non-linear data, integrating the geometric mean into analytical frameworks will enhance the robustness of research findings, ensuring that interpretations remain grounded in statistical reality. Future studies should explore hybrid approaches, combining geometric means with other measures to capture the multifaceted nature of social phenomena.
Highly Recommended Books
- Statistics for Research: With a Guide to Spss – Amazon Link – https://amzn.to/4ksD60I
- Statistics for the Social Sciences by Sirkin R. Mark – Amazon Link – https://amzn.to/4kBe7bP
- Statistical Methods by Aggarwal – Amazon Link – https://amzn.to/4jkIfY0
Topic Related Questions
5-Mark Questions (Short Answer)
- Define geometric-mean and provide its mathematical formula.
- Why is the geometric-mean preferred over the arithmetic mean in income distribution studies?
- Give an example where the geometric-mean is used in social research.
- What is the main limitation of the geometric-mean when dealing with zero or negative values?
- How does the geometric-mean help in analyzing population growth rates?
10-Mark Questions (Brief Explanation/Essay)
- Explain how the geometric-mean is used to measure income inequality, with an example.
- Compare the geometric-mean with the arithmetic mean and median in the context of social research.
- Discuss the role of the geometric-mean in constructing composite social indices like the Human Development Index (HDI).
- Why is the geometric-mean suitable for log-normal distributions? Provide a sociological example.
- How does the geometric-mean improve the analysis of skewed data in urban sociology?
15-Mark Questions (Detailed Analysis/Case Study)
- Critically evaluate the advantages and disadvantages of using the geometric-mean in sociological research, with real-world examples.
- “The geometric-mean provides a more realistic measure of central tendency in highly unequal societies.” Discuss this statement with reference to wealth distribution studies.
- Explain how the geometric-mean is applied in demographic and health research. Use case studies on disease spread or vaccination rates.
- How can the geometric mean be integrated into policy-making for economic development? Discuss with examples from social development indices.
- Compare the use of geometric-mean, arithmetic mean, and harmonic mean in migration and population density studies. Which is most effective and why?
Additional Discussion-Based Questions
- “Should the geometric-mean replace the arithmetic mean in all social research?” Argue for or against this statement.
- How does the geometric-mean address the limitations of other averages in gender wage gap studies?
- Can the geometric-mean be used in qualitative sociological research? Justify your answer.

1 thought on “Understanding Geometric Mean in Social Research: A Sociological Perspective”